staircase.Stairs.corr

Stairs.corr(other, lower=-inf, upper=inf, lag=0, clip='pre')

Calculates either correlation, autocorrelation or cross-correlation.

All calculations are based off the Pearson correlation coefficient.

The calculation is between two step functions described by self and other. If lag is None or 0 then correlation is calculated, otherwise cross-correlation is calculated. Autocorrelation is a special case of cross-correlation when other is equal to self.

Parameters:

• other (Stairs) – the stairs instance with which to compute the correlation
• lower (int, float or pandas.Timestamp) – lower bound of the interval on which to perform the calculation
• upper (int, float or pandas.Timestamp) – upper bound of the interval on which to perform the calculation
• lag (int, float, pandas.Timedelta) – a pandas.Timedelta is only valid when using dates. If using dates and delta is an int or float, then it is interpreted as a number of hours.
• clip ({'pre', 'post'}, default 'pre') – only relevant when lag is non-zero. Determines if the domain is applied before or after other is translated. If ‘pre’ then the domain over which the calculation is performed is the overlap of the original domain and the translated domain.

Returns:

The correlation (or cross-correlation) between self and other

Return type:

float

See also

Stairs.cov(), staircase.corr(), staircase.cov()

Examples

>>> fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12,5), sharey=True, sharex=True)
>>> for ax, title, stair_instance in zip(axes, ("s1", "s2"), (s1, s2)):
...     stair_instance.plot(ax, label=title)
...     ax.set_title(title)

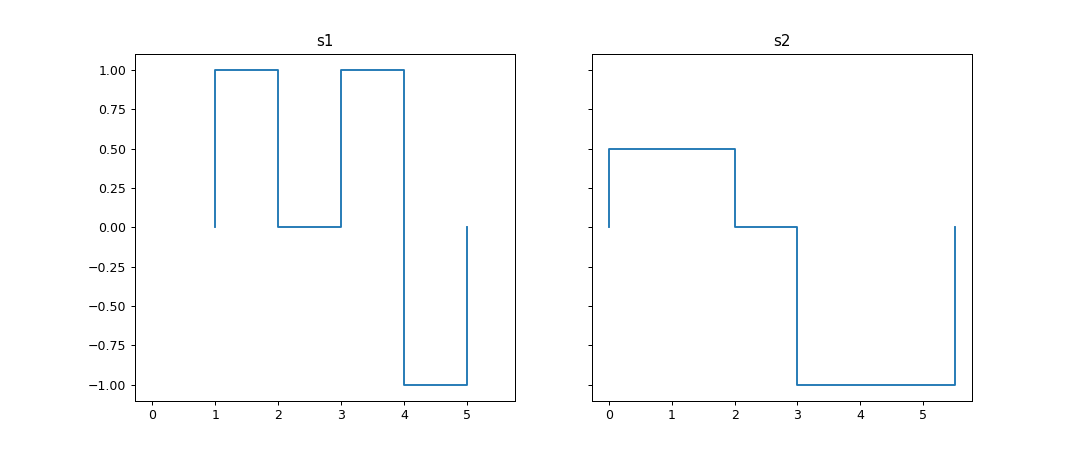
>>> s1.corr(s2)
0.24687803791136045

>>> s2.corr(s1)
0.24687803791136045

>>> s1.corr(s2, lower=0, upper=6)
0.27500954910846337

>>> # autocorrelation with lag 1
>>> s1.corr(s1, lower=1, upper=5, lag=1)
-0.8660254037844386

>>> # cross-correlation with lag 1
>>> s1.corr(s2, lower=1, upper=5.5, lag=1)
0.4961389383568339

>>> # cross-correlation with lag 1
>>> s1.corr(s2, lower=1, upper=4.5, lag=1, clip='post')
0.4961389383568339