staircase.Stairs.sample¶
-
Stairs.sample(x, how='right', aggfunc=None, window=(0, 0), lower_how='right', upper_how='left')¶ Evaluates the value of the step function at one, or more, points.
This method can be used to directly sample values of the corresponding step function at the points provided, or alternatively calculate aggregations over some window around each point. The first of these is performed when aggfunc is None.
If aggfunc is None then the results of this function should be considered as \(\lim_{x \to z^{-}} f(x)\) or \(\lim_{x \to z^{+}} f(x)\), when how = ‘left’ or how = ‘right’ respectively. See A note on interval endpoints for an explanation.
If aggfunc is not None then a window, around each point x (referred to as the focal point), over which to aggregate is required. The window is defined by two values paired into an array-like parameter called window. These two scalars are the distance from the focal point to the left boundary of the window, and the right boundary of the window respectively.
The function can be called using parentheses. See example below.
Parameters: - x (int, float or vector data) – Values at which to evaluate the function
- how ({'left', 'right'}, default 'right') – Only relevant if aggfunc is None. If points where step changes occur do not coincide with x then this parameter has no effect. Where a step changes occurs at a point given by x, this parameter determines if the step function is evaluated at the interval to the left, or the right.
- aggfunc ({'mean', 'median', 'mode', 'max', 'min', 'std', None}. Default None.) – A string corresponding to the aggregating function
- window (array-like of int, float or pandas.Timedelta, optional) – Only relevant if aggfunc is not None. Should be length of 2. Defines distances from focal point to window boundaries.
- lower_how ({'left', 'right'}, default 'right') – Only relevant if aggfunc is not None. Determines how the left window boundary should be evaluated. If ‘left’ then \(\lim_{x \to lower_how^{-}} f(x)\) is included in the window.
- upper_how ({'left', 'right'}, default 'left') – Only relevant if aggfunc is not None. Determines how the right window boundary should be evaluated. If ‘right’ then \(\lim_{x \to upper_how^{+}} f(x)\) is included in the window.
Returns: Return type: float, or list of floats
See also
Examples
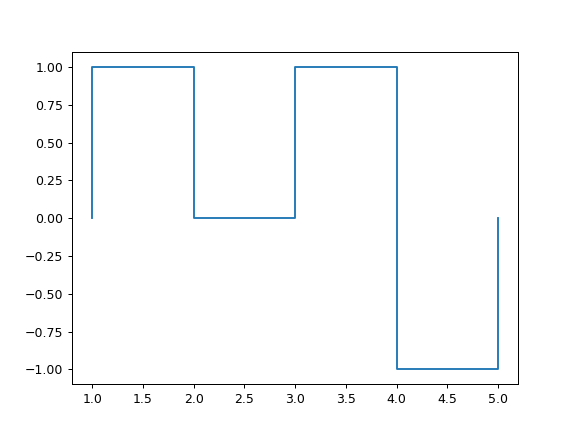
>>> s1.plot() >>> s1(3.5) 1 >>> s1([1, 2, 4.5, 6]) [1, 0, -1, 0] >>> s1([1, 2, 4.5, 6], how="left") [0, 1, -1, 0] >>> s1([1, 2, 4.5], aggfunc="mean", window=(-0.5, 0.5)) [0.5, 0.5, -1.0] >>> s1([1, 2, 4.5], aggfunc="max", window=(-0.5, 0.5)) [1, 1, -1] >>> s1([1, 2, 4.5], aggfunc="max", window=(-0.5, 0.5), lower_how="left") [1, 1, 1] >>> s1([1, 2, 4.5], aggfunc="max", window=(-0.5, 0.5), upper_how="right") [1, 1, 0]