A note on interval endpoints#
In general, it is possible for the disjoint intervals comprising a step function to be closed, half-closed or open. However the internals of staircase package do not explicitly model which interval endpoints are open and which are closed - and do not explicitly model the value of the step function at the interval endpoints. Does this mean we cannot use staircase to evaluate a step function f at interval endpoints? Not quite. The internals of staircase permit \(\lim_{x \to z} f(x)\) to be calculated, so under certain assumptions the value at interval endpoints can be inferred:
if f is comprised of only left-closed intervals then \(f(z) = \lim_{x \to z^{+}} f(x)\) for all z (including interval endpoints)
if f is comprised of only right-closed intervals then \(f(z) = \lim_{x \to z^{-}} f(x)\) for all z (including interval endpoints)
To simplify explanation, we refer to step functions comprising of only left-closed intervals, as left-closed step functions, and extend the same concept to right-closed step functions.
In staircase v1 it was suggested that users make an assumption to work with either left-closed step functions, or right-closed step functions. In staircase v2 this assumption is made explicit at the time of initialising staircase.Stairs instances via the closed parameter. Consider the following example:
In [1]: import staircase as sc
In [2]: import matplotlib.pyplot as plt
In [3]: sf1 = sc.Stairs(closed="left").layer(0, 1)
In [4]: sf2 = sc.Stairs(closed="right").layer(0, 1)
In [5]: fig, axes = plt.subplots(ncols=2, figsize=(7,3), sharex=True, sharey=True)
In [6]: sf1.plot(ax=axes[0], arrows=True);
In [7]: axes[0].set_title("sf1 (left-closed)");
In [8]: sf2.plot(ax=axes[1], arrows=True);
In [9]: axes[1].set_title("sf2 (right-closed)");
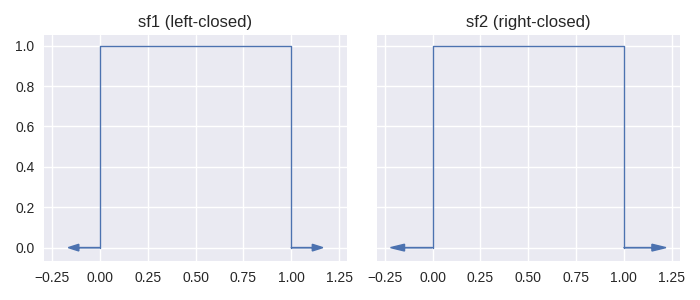
It should be clear that whether a step function in staircase is left-closed, or right-closed, cannot be deduced from the plotting function. Let’s see how it makes a difference when sampling:
In [10]: sf1([0, 0.5, 1])
Out[10]: array([1, 1, 0])
In [11]: sf2([0, 0.5, 1])
Out[11]: array([0, 1, 1])
Note that the closed parameter has a default value of “left”. This is motivated by the fact that time based intervals, such as hours, days and years, are left-closed. Once a staircase.Stairs object has been created it cannot change from left-closed to right-closed, and vice versa.