Gotchas#
A “gotcha” is any feature of the programming language, which works as intended, but can result in an unexpected result. Below we discuss and describe the two gotchas that can arise when using staircase.
Null values in staircase.Stairs.layer parameters start and end
Let’s start with the simplest case, when start = end = None, that is what is the result of .layer()?
In The layer method it states that a null value in the start parameter corresponds to negative infinity and a null value in the end parameter corresponds to positive infinity. Consider the following step function where x is a number:
sc.Stairs().layer(-x,x)
The resulting Stairs instance has value 1 between -x and x, and value 0 everywhere else. As x approaches infinity, the step function approaches a horizontal line with value 1. Hence the result of .layer() is equivalent to increasing every value of the step function by 1. In general .layer(value=n) is equivalent to adding n to the step function.
Where this becomes a “gotcha” is when start or end are vectors which contain null values. Consider the following:
In [1]: df
Out[1]:
start end
0 5.0 NaN
1 NaN 2.0
2 NaN NaN
In [2]: fig, axes = plt.subplots(ncols=2, figsize=(7,3), sharex=True, sharey=True)
In [3]: sc.Stairs().layer("start", "end", frame=df[:-1]).plot(axes[0], arrows=True);
In [4]: axes[0].set_title("frame=df[:-1]")
Out[4]: Text(0.5, 1.0, 'frame=df[:-1]')
In [5]: sc.Stairs().layer("start", "end", frame=df).plot(axes[1], arrows=True);
In [6]: axes[1].set_title("frame=df")
Out[6]: Text(0.5, 1.0, 'frame=df')
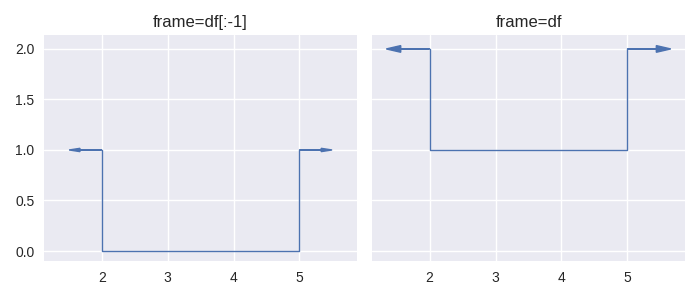
As can be seen from the plots above, the last row of the dataframe, which contains null values for start and end, raises the step function. Whether this behaviour is desirable depends on how the null values have come to exist. If each row of the dataframe corresponds to an event, marked by a start time and an end time, then are four possible reasons for these values to be null:
The event started prior to data logging, and ended after data logging
The event started, and ended, prior to data logging
The event started, and ended, after data logging
The event never exists
Of all the possibilities, 1) is the only one for which the staircase.Stairs.layer() method will give the desired results. The lesson learned here is users must be wary of missing values in their data and how they were generated. Sometimes the right course of action will be to remove them, sometimes it won’t.
Statistical calculations on "unclipped" step functions
This gotcha arises with several statistical calculations using staircase however let’s first examine integral and mean. Integral and mean calculations for functions are related, and the latter relies on the former. In maths, (definite) integral calculations are specified with a domain (a,b): \(\int_{a}^{b} f(x) \,dx\). In staircase the integral calculation is performed over the entire domain, i.e. \((a,b) = (-\inf, \inf)\). This is known as an “improper integral”. However if the step function has been clipped at points (a,b) then it is undefined outside of this interval and \(\int_{-\inf}^{\inf} f(x) \,dx = \int_{a}^{b} f(x) \,dx\). If the step function is not clipped, then it may have intervals, with non-zero values, which extend to negative infinity or positive infinity. An integral calculation over the entire domain in such cases is undefined *. Consequently staircase ignores these infinite length intervals. To make the behaviour clear, we state the following statements are equivalent:
When calculating an integral:
any infinite length interval is ignored
any infinite length interval is assumed to be zero valued
the step function is first clipped at the finite endpoint of any infinite length interval
To see how the gotcha arises consider the following example with two step functions:
In [7]: sf1 = sc.make_test_data(seed =1).pipe(sc.Stairs, "start", "end")
In [8]: sf2 = sc.make_test_data(seed =2).pipe(sc.Stairs, "start", "end")
In [9]: ax = sf1.plot(color="red", label="sf1")
In [10]: sf2.plot(ax, color="blue", label="sf2");
In [11]: ax.legend()
Out[11]: <matplotlib.legend.Legend at 0x7f7c251b22e0>
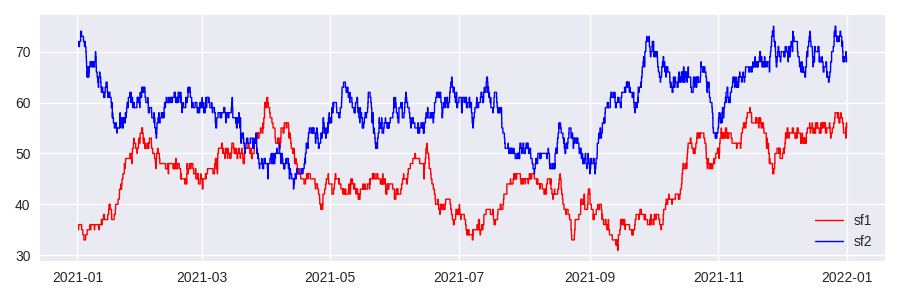
When looking at these plots it can be easy to forget that each of these step functions has intervals which extend to negative infinity and positive infinity. From the plot we can see that step function sf1 is very rarely larger than sf2. What if we want to know how often this occurs, as a fraction of the year 2021? This is achieved with the staircase.Stairs.mean() method:
In [12]: (sf1 > sf2).mean()
Out[12]: 0.7786321327397815
We can see from the graph that sf1 is certainly not larger than sf2 ~78% of the time! Is this result surprising? If so, then this is the gotcha in action. Inspecting the step function which results from the comparison, using staircase.Stairs.to_frame(), shows that step function has infinite intervals extending from 2021-03-21 15:08:00 to negative infinity and from 2021-04-16 08:53:00 to positive infinity. Any integral or mean calculation is performed over the domain (2021-03-21 15:08:00, 2021-04-16 08:53:00) and not the entire year as required.
To achieve the desired result the step function should be clipped to the required domain before calculating:
In [13]: year2021 = (pd.Timestamp("2021"), pd.Timestamp("2022"))
In [14]: (sf1 > sf2).clip(*year2021).mean()
Out[14]: 0.05490867579908676
or, perhaps preferably, the original step functions are clipped:
In [15]: sf1 = sf1.clip(*year2021)
In [16]: sf2 = sf2.clip(*year2021)
In [17]: (sf1 > sf2).mean()
Out[17]: 0.05490867579908676
Reminder: although the example above is illustrated with mean and integral, every statistical function in staircase suffers a similar gotcha. The lesson learned here, is always clip step functions before calculating statistics.
Footnotes
- *
Technically an improper integral can be evaluated if there exists c such that \(\int_{-\inf}^{c} f(x) \,dx\) and \(\int_{c}^{\inf} f(x) \,dx\) are convergent. For step functions this requires either infinite length intervals are zero valued, or an infinite number of intervals (which is not supported by
staircase).