Case study: queue analysis#
This case study illustrates the use of the staircase package for queue analysis. In this example vessels (i.e. ships) arrive offshore and await their turn to enter a harbour where they will be loaded with cargo. We will examine the queue, which is composed of all vessels which is offshore but yet to enter the harbour, for the year 2020.
We begin by importing the queue data into a pandas.DataFrame where each row corresponds to a vessel. The first column gives the time at which the vessel arrives offshore (enters the queue), and the second column gives the time at which the vessel enters the harbour (leaves the queue). A NaT value in either of these columns indicates the vessel entered the queue prior to 2020, or left the queue after 2020, however this approach does not require these values to be NaT. The third column gives the weight, in tonnes, of cargo destined for the vessel. Note, for this approach we require every vessel, that was in the queue at some point in 2020, to appear in the dataframe.
In [1]: import pandas as pd
In [2]: import staircase as sc
In [3]: import matplotlib.pyplot as plt
In [4]: data = pd.read_csv(vessel_data, parse_dates=["enter", "leave"], dayfirst=True)
In [5]: data
Out[5]:
enter leave tonnes
0 NaT 2020-01-01 04:40:00 129000
1 NaT 2020-01-01 22:18:00 69055
2 NaT 2020-01-01 11:47:00 138000
3 NaT 2020-01-02 10:12:00 84600
4 NaT 2020-01-01 22:39:00 142550
... ... ... ...
1224 2020-12-29 05:59:00 NaT 142500
1225 2020-12-29 17:41:00 NaT 84600
1226 2020-12-30 12:41:00 NaT 119200
1227 2020-12-30 16:59:00 NaT 113200
1228 2020-12-30 17:59:00 NaT 142500
[1229 rows x 3 columns]
A step function, which quantifies the size of the queue, can be created with vector data corresponding to start and end times for the state being modelled. In this case, where the state is “in the queue”, the required data is the columns “enter” and “leave”. Note that since we want to examine 2020 we clip the step function at the year endpoints, making the functions undefined for any time outside of 2020 (see Gotchas for why this is a good idea).
In [6]: queue = sc.Stairs(frame=data, start="enter", end="leave")
In [7]: queue = queue.clip(pd.Timestamp("2020"), pd.Timestamp("2021"))
In [8]: queue.plot();
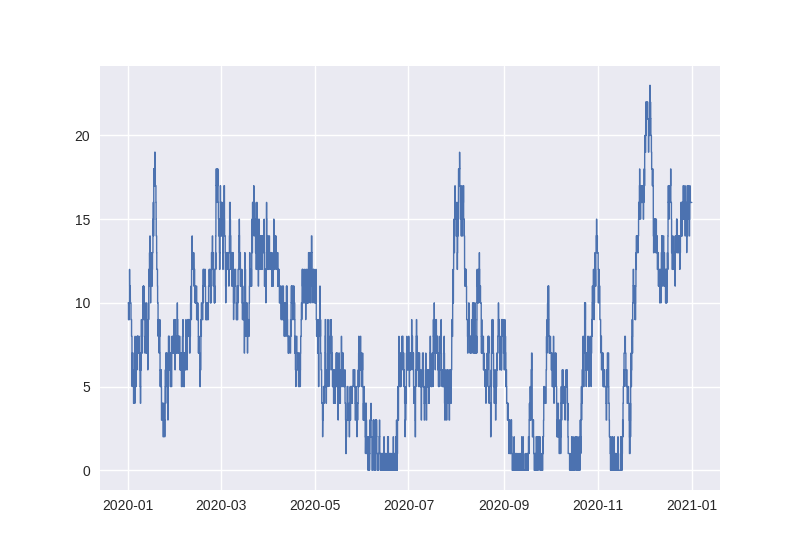
From the chart it would appear the size of the queue at the beginning of 2020 is around 10 vessels. This can be confirmed by calling the step function with this time as an argument - a deliberate choice to emulate the notation for evaluating a function at a particular point:
In [9]: queue(pd.Timestamp("2020-01-01"))
Out[9]: 10.0
Assuming that no vessels arrive precisely at midnight on the 1st of Jan, we can expect the number of vessels in the queue at this time to be equal to the number of NaT values in the “enter” column:
In [10]: data["enter"].isna().sum()
Out[10]: 10
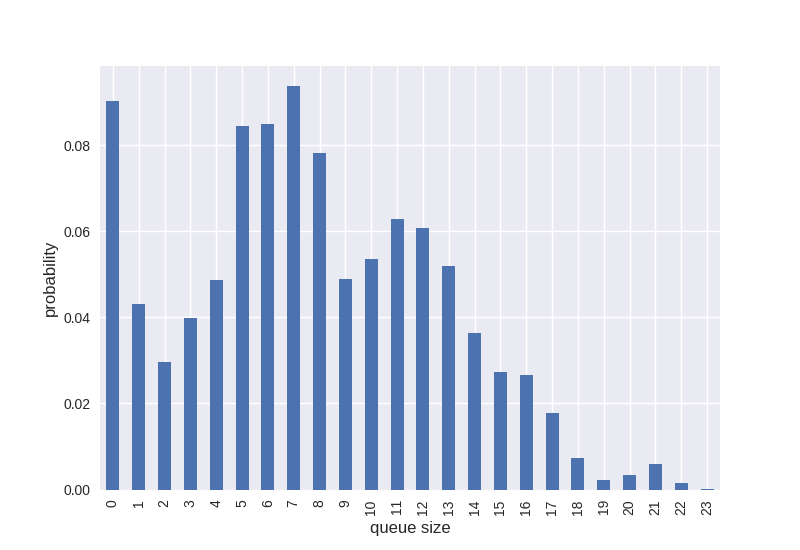
There are a number of ways we can characterise the distribution of the queue size values. The staircase.Stairs.hist() method creates histogram data as a pandas.Series, indexed by a pandas.IntervalIndex. If the bins parameter is not supplied then the method will use unit bins which cover the range of the step function values:
In [11]: queue_hist = queue.hist(stat="probability")
In [12]: queue_hist
Out[12]:
[0, 1) 0.090418
[1, 2) 0.043205
[2, 3) 0.029688
[3, 4) 0.039870
[4, 5) 0.048759
[5, 6) 0.084548
[6, 7) 0.085024
[7, 8) 0.093790
[8, 9) 0.078144
[9, 10) 0.048905
[10, 11) 0.053679
[11, 12) 0.062805
[12, 13) 0.060775
[13, 14) 0.051981
[14, 15) 0.036320
[15, 16) 0.027256
[16, 17) 0.026677
[17, 18) 0.017746
[18, 19) 0.007252
[19, 20) 0.002284
[20, 21) 0.003338
[21, 22) 0.005897
[22, 23) 0.001510
[23, 24) 0.000127
dtype: float64
Given the queue length is integer variable the pandas.IntervalIndex can be replaced to produce a simpler plot:
In [13]: queue_hist.index = queue_hist.index.left
In [14]: ax = queue_hist.plot.bar()
In [15]: ax.set_xlabel("queue size", fontsize="12")
Out[15]: Text(0.5, 0, 'queue size')
In [16]: ax.set_ylabel("probability", fontsize="12")
Out[16]: Text(0, 0.5, 'probability')
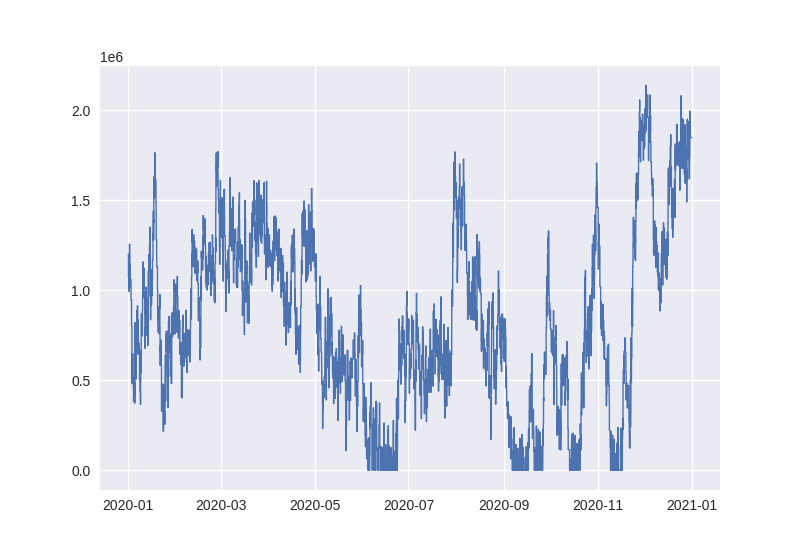
Another useful queue metric in the context of this case study is “queue tonnes”. This metric is calculated as the sum of the cargo tonnes destined for vessels in the queue. Since the queue is a step function, queue tonnes must also be a step function. The creation of a queue tonnes step function is similar to that used for the queue, but requires the vector of cargo tonnes to be used in construction. The value parameter, which defaults to a vector of ones, indicates how much the step function should increase or decrease whenever the corresponding vessels enter or leave the queue:
In [17]: queue_tonnes = sc.Stairs(frame=data, start="enter", end="leave", value="tonnes")
In [18]: queue_tonnes = queue_tonnes.clip(pd.Timestamp("2020"), pd.Timestamp("2021"))
In [19]: queue_tonnes.plot();
Before diving deeper into distributions we tackle a variety of miscellaneous questions for the purposes of demonstration.
What was the maximum queue tonnes in 2020?
In [20]: queue_tonnes.max()
Out[20]: 2138466.0
What was the average queue tonnes in 2020?
In [21]: queue_tonnes.mean()
Out[21]: 817852.320958561
What fraction of the year was the queue_tonnes larger than 1.5 million tonnes?
In [22]: (queue_tonnes > 1.5e6).mean()
Out[22]: 0.09867751973284761
What was the median queue tonnes for March?
In [23]: queue_tonnes.clip(pd.Timestamp("2020-3"), pd.Timestamp("2020-4")).median()
Out[23]: 1281300.0
What is the 80th percentile for queue tonnes?
In [24]: queue_tonnes.percentile(80)
Out[24]: 1265100.0
What is the 40th, 65th, 77th and 90th percentiles for queue tonnes?
In [25]: queue_tonnes.percentile([40,65,77,90])
Out[25]: array([ 659500., 1035400., 1220600., 1496800.])
Aside from being able to evaluate any number of percentiles, we can plot the “percentile function”:
In [26]: queue_tonnes.percentile.plot()
Out[26]: <AxesSubplot: >
The percentile function is essentially the inverse of an empirical cumulative distribution function. We can generate an ecdf for the step function values too:
In [27]: queue_tonnes.ecdf.plot()
Out[27]: <AxesSubplot: >
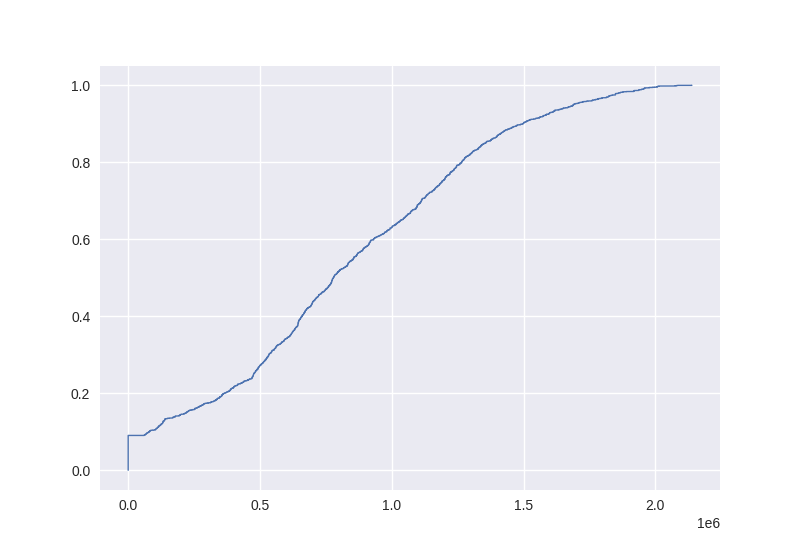
Earlier we found that the queue tonnes were strictly above 1.5Mt about 9.87% of the time. The ecdf can tell us what fraction of the time the queue tonnes was less than or equal to 1.5Mt. (We’d expect these results to add to 1).
In [28]: queue_tonnes.ecdf(1.5e6)
Out[28]: 0.9013224802671552
We can also then discover the fraction of time that 1Mt < queue tonnes <= 1.5Mt like so:
In [29]: queue_tonnes.ecdf(1.5e6) - queue_tonnes.ecdf(1e6)
Out[29]: 0.2707840012143298
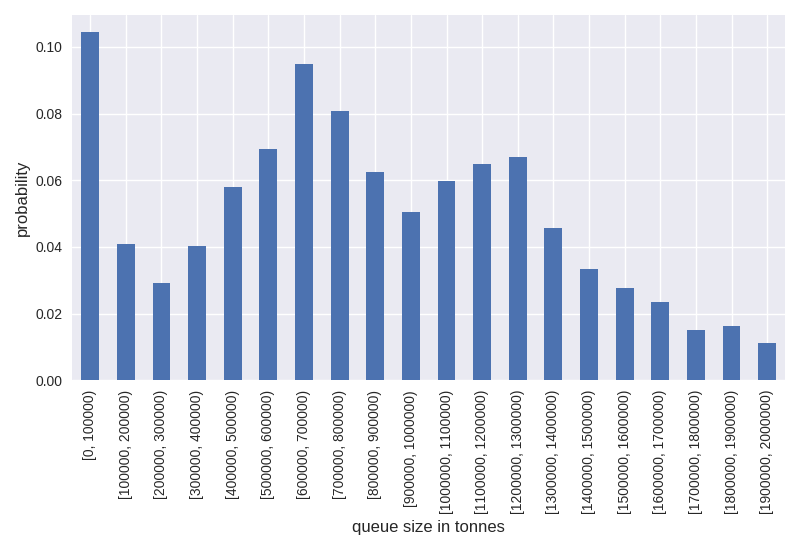
This piece of data is tantamount to a single bin in histogram data. Earlier we used the staircase.Stairs.hist function on the queue length, with default bin sizes. Since the range of the queue tonnes values is much larger it will be useful to specify the bins (defined by the edges) to generate a histogram for the queue tonnes.
In [30]: queue_tonnes_hist = queue_tonnes.hist(bins = range(0, 2100000, 100000), stat="probability")
In [31]: queue_tonnes_hist
Out[31]:
[0, 100000) 0.104360
[100000, 200000) 0.040817
[200000, 300000) 0.029093
[300000, 400000) 0.040346
[400000, 500000) 0.057899
[500000, 600000) 0.069479
[600000, 700000) 0.094911
[700000, 800000) 0.080645
[800000, 900000) 0.062583
[900000, 1000000) 0.050406
[1000000, 1100000) 0.059751
[1100000, 1200000) 0.064855
[1200000, 1300000) 0.066940
[1300000, 1400000) 0.045719
[1400000, 1500000) 0.033519
[1500000, 1600000) 0.027588
[1600000, 1700000) 0.023567
[1700000, 1800000) 0.014984
[1800000, 1900000) 0.016359
[1900000, 2000000) 0.011215
dtype: float64
As we did earlier for the queue length histogram, we can quickly create a chart with pandas Series plotting functions.
In [32]: ax = queue_tonnes_hist.plot.bar()
In [33]: ax.set_xlabel("queue size in tonnes", fontsize="12")
Out[33]: Text(0.5, 0, 'queue size in tonnes')
In [34]: ax.set_ylabel("probability", fontsize="12")
Out[34]: Text(0, 0.5, 'probability')
In [35]: plt.tight_layout()
Although there is plenty of analysis achieveable through step functions, it may be desirable to aggregate the data to a traditional time series - a daily mean for example. This can be achieved with SLICING
In [36]: day_range = pd.date_range("2020", freq="D", periods=366)
In [37]: queue_tonnes.slice(day_range).mean()
Out[37]:
[2020-01-01, 2020-01-02) 1.100435e+06
[2020-01-02, 2020-01-03) 1.052939e+06
[2020-01-03, 2020-01-04) 7.316999e+05
[2020-01-04, 2020-01-05) 4.992351e+05
[2020-01-05, 2020-01-06) 5.410560e+05
...
[2020-12-26, 2020-12-27) 1.807232e+06
[2020-12-27, 2020-12-28) 1.729369e+06
[2020-12-28, 2020-12-29) 1.680614e+06
[2020-12-29, 2020-12-30) 1.870018e+06
[2020-12-30, 2020-12-31) 1.733728e+06
Length: 365, dtype: float64